
I recently learned that this year’s Nobel Prize in Physics went to a team of scientists who conducted experiments on quantum tunneling. Their experiments were conducted in the 1980s, which is typical of how the Nobel committees work—it takes around thirty years for a scientific consensus to build that a body of work was truly worthy of a Nobel Prize.
I was interested in this news because, like most sci-fi nerds, I have an unflagging fascination with quantum mechanics. Heck, I even have a passing understanding of the fundamentals. (No, not just from Star Trek; I’ve read a few actual books! With facts, and stuff!) A few years ago, I even tried to write a non-fiction book about Bell’s Theorem, which is a famous consent in Quantum Mechanics, albeit one that you’ve probably never heard of (unless you’re a physicist or a science teacher or a sci-fi nerd).

To be frank, I had never heard of it either, until I read about it in a science book and then ventured to the Wikipedia page, where I learned that the theorem was written by an Anglo-Irish physicist named John Stewart Bell in the 1960s, and it hit the scientific community like a hurricane. Later, in 1975, another physicist Henry Stapp called it “the most profound discovery of science.”
When I read this quote, I thought, “Whoa, dude! If it’s really the most ‘profound discovery of science’,” I should probably learn something about it.”
And I did. Sort of.
Obviously, I will never really understand the underlying math, or even the root concepts that the math represents (which is one reason I abandoned the aforementioned book project). But the theorem itself is pretty easy to understand….
Imagine you have a drawer full of socks. Some of the socks are long and some are short. Some are white and some are black. And all combinations of these properties (length, color) are represented. Also, imagine that each time you do laundry, you fold the socks into those tight, little grenade pairs so that you don’t have to go fumbling for a match each morning.
Unfortunately, you have a mischievous teenager in the house. Said teenager secretly comes into your room one night, undoes all the grenades, and remakes them—only this time, instead of matching socks on color and length, the little brat makes sure that the pairs never match on either of these properties. That is, a short sock can only be matched with a long sock, and a white sock can only be matched with a black sock.
The next day, you discover the trick. Nevertheless, you decide to continue with a long-planned experiment. You put on a blindfold, reach into the drawer, and get out one (mismatched) sock grenade. With the blindfold still on, you unwind the grenade and put one sock in a little cardboard box and the other sock in another box. You seal both boxes. Then, (you can take the blindfold off now), you drive the boxes to FedEx and mail one to your friend Alice in New York and the other to your friend Bob in Los Angeles.
When your friends get their packages, each does an experiment. Actually, they have a choice of doing one of two possible experiments: they can either X-Ray the box and see if the sock inside is long or short (but they can’t see its color), OR they can open the box lid just a sliver and see if the sock inside is black or white (but they can’t see its length). It’s totally up to Alice and Bob to choose which of these two tests to use (they might even flip a coin to decide, making it totally random). When each test is done, the results are tallied as follows: If the sock is white, the result is 1; if black, -1. If the sock is long, the result is 1: if short, -1. Alice and Bob then send you an email, telling you which test they chose and their (1 or -1) result.
Now, if all this sock-drawer rigmarole seems pointless and complicated, bear with me.
One thing you might have noticed about this experiment is that the moment Alice or Bob conducts their experiment, they can instantly realize something about the other friend’s sock-in-a-box. Namely, Alice knows that if she got a white sock, then Bob got a black sock; if she got a short sock, then Bob got a long sock. And vice-versa and verse-visa.
This instantaneous quality of their respective realizations is true whether they are on opposite sides of North America or of the Milky Way galaxy. It doesn’t matter. And while, to a naive observer, this realization might seem to suggest that some kind of faster-than-light communication has occurred between Alice and Bob, we know that this is merely an illusion. The blackness/whiteness and shortness/longness of the sock was already decided when the socks first went into their boxes in your bedroom; the friends just couldn’t see it. (This secret-but-already-decided quality is called a hidden variable by physicists in discussions of such things.)
John Bell’s great idea was to use, instead of socks, two electrons. And not just any two electrons, mind you, but a pair that have been emitted together in such a way that they are entangled at the quantum level. And, in Bell’s hypothetical experiment, you use some quantum-mechanical (and entangled) properties like spin on the x-axis or y-axis instead of sock length/color. Then, you can run the same experiment hundreds of times, with Bob and Alice once again emailing you their results.
Again, as with the socks, each time Alice or Bob makes one of their (single, randomly chosen) tests, they instantaneously know something about the other’s sock (er…electron), thanks to the quantum entanglement. So, if Alice sees that her electron has an x-axis spin of 1, then she knows that Bob’s has a x-axis spin of -1. And if Bob’s electron has a y-axis spin of 1, he knows that Alice’s has a value of -1. (The converse, reverse, and observe, and Marvel Comics Multiverse are also true. I think.)
But here’s the kicker….
Unlike socks-in-boxes, the spin values of quantum entangled electrons is not something that can be said to truly exist until it is measured. Rather, it exists in a state of quantum superposition, literally being both true and false, up and down, black and white, at the same time. This duality remains until the particle’s spin is pinpointed and observed, at which time this quantum state collapses and the value is seen to have one or the other value.
Just as Schrödinger’s famous cat is both alive and dead until you look in its quantum box and see, so the electron has both 1 and -1 spin until you measure it. And, when Alice does finally measure it, she instantaneously knows the value of the other (Bob’s) particle.
This presto-chango quality of quantum mechanics (i.e., actions that can have effects which propagate faster than the speed-of-light) is something that orthodox physicists found very hard to swallow, back in the day. After all, this so-called “spooky action at a distance” violated the hitherto sacrosanct Principle of Locality, which holds that actions can never affect objects outside their immediate vicinity (i.e., not further away than a beam of light could travel in the given timeframe).
In fact, in the early days of Quantum Theory, many older, classical physicists like Einstein simply refused to believe that such a thing as superposition was possible. They insisted that there must be some hidden-variable involved. Like the mischievous teenager in our socks-in-boxes scenario, there must be some pre-decided aspect to electron spin, an actual binary value that, while temporarily hidden from humanity (and perhaps even from God), still exists in some independent, literal, epistemological, cosmological, and for-all-we-know scatological sense.
So, who is right? And how do you tell? How do you look at the sock in the box without looking at the sock inside the box?
As it turns out, John Bell found a way.
If you abbreviate Alice as A and Bob as B and the color test as c and length test as l, you can keep track of the results using the following codes:
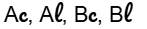
Let’s say that you repeat the sock experiment hundreds of times, keeping a tally of these four possible test results. Let’s alos say that you make an Excel spreadsheet with these four columns (Ac, Al, Bc, Bl), putting in a new row for each day you run the experiment. (Note that on any given day, you will only fill out two of those columns since Alice and Bob only run one of their two possible tests each time. For the other values, you just leave them blank for that day.) At the bottom of the sheet, you keep a running average of each column.
Now, if you plug in these four averages (denoted by angle-brackets: 〈〉) into the clever algebraic equation below that Bell came up up with (and which I won’t explain here because I don’t really understand it), one can calculate that, over time, the absolute value will be less than or equal to 2:

Okay, you think, great. So what?
Well, the amazingly cool think that Bell figured out is that if you use electrons instead of socks and electron spins instead of color/length (or whatever classical property you choose to measure), and if you re-run the experiment hundreds of times and plug the averages into the same equation, you will arrive at a different number. Specifically, over time, you will get a number greater than 2.
The reason for this is that the terms in the equation do not cancel each other out the same way in quantum mechanics as they do in classical mechanics. This was Bell’s great stroke of genius. More importantly, it gave physicists a potential, practical way to look inside the quantum box without looking in the box.
Once and for all, we could settle the Einstein/Heisenberg argument.
Of course, it wasn’t until 1982 that a French physicist with the incredibly metal name of Alain Aspect built a machine that could actually perform an practical experiment based on Bell’s ideas. It used photons instead of electrons, and three spin-values instead of two. The results found that no hidden variables were involved, thus confirming the concept of superposition. (Aspect won the 2022 Nobel Prize in Physics for his work.)

Actually, the experimental results found by Aspect, and others since him, do not completely rule out the hidden-variables idea. There is one possible loophole: superdeterminism. This is the idea that everything in the experiment above, including Alice’s and Bob’s choice of tests, is pre-determined. In fact, superdeterminism implies that everything in the universe, down to the most minute motion of each sub-atomic particle is knowable in advance, eliminating even the merest possibility of free will in conscious beings like us. As Bell himself explained it:
There is a way to escape the inference of superluminal speeds and spooky action at a distance. But it involves absolute determinism in the universe, the complete absence of free will. Suppose the world is super-deterministic, with not just inanimate nature running on behind-the-scenes clockwork, but with our behavior, including our belief that we are free to choose to do one experiment rather than another, absolutely predetermined, including the “decision” by the experimenter to carry out one set of measurements rather than another, the difficulty disappears. There is no need for a faster than light signal to tell particle A what measurement has been carried out on particle B, because the universe, including particle A, already “knows” what that measurement, and its outcome, will be.
This might seem like an absurd, even insane idea, but it’s really not that far from the religious thinking of the reformation like that of John Calvin.
I, for one, totally reject the notion of predestination on philosophical, metaphysical, and moral grounds. Fortunately, most physicists doubt it, too. As Anton Zeilinger wrote,
[W]e always implicitly assume the freedom of the experimentalist… This fundamental assumption is essential to doing science. If this were not true, then, I suggest, it would make no sense at all to ask nature questions in an experiment, since then nature could determine what our questions are, and that could guide our questions such that we arrive at a false picture of nature.
In other words, once you put superdetermination on the table, all bets are off. You can’t be sure of anything anymore, not even the ability of your own consciousness to choose, conduct, and interpret scientific experiments.
So, you see, Bell’s Theorem is not just an incredibly cool scientific discovery. It actually butts up against ideas of free will, humanism, and even consciousness. It leaves all kinds of doors open, through which all the old and continuing hopes of humanity can—just possibly—squeeze through.
